Radiazione di dipolo elettrico

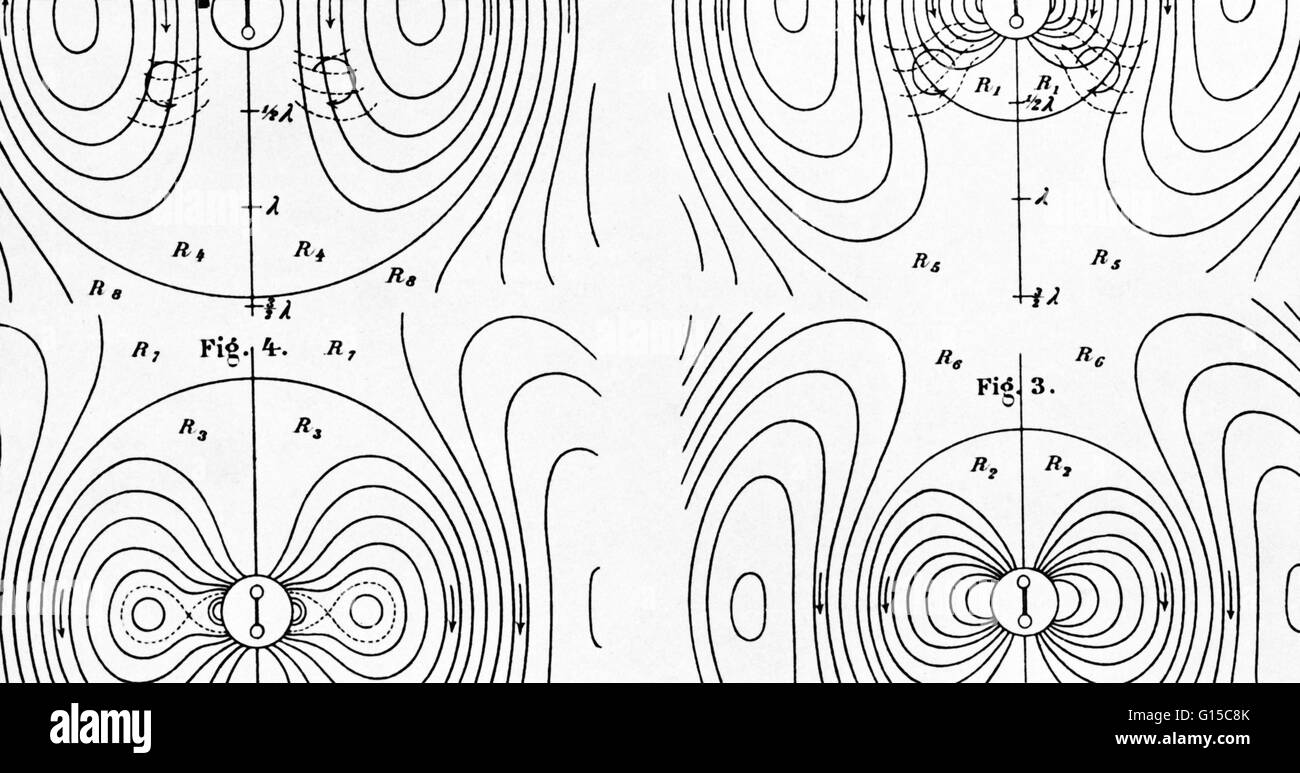
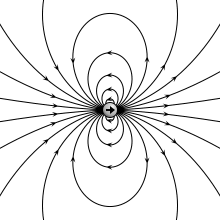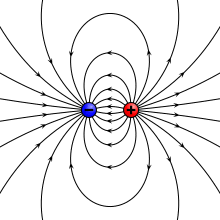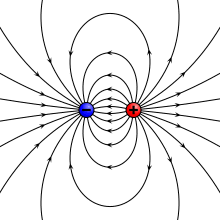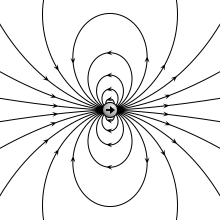
In fisica, la radiazione di dipolo elettrico è la radiazione elettromagnetica prodotta da un dipolo elettrico accelerato. Se oscillante è detto, solitamente, dipolo oscillante o antenna dipolare.

Lo studio del dipolo elettrico si basa sullo sviluppo in multipoli del potenziale elettrico generato da una distribuzione di carica e corrente oscillante nel tempo.

Espressione dei campi

La descrizione della radiazione prodotta dal dipolo è basata sull'espressione dei potenziali ritardati, che vengono definiti a partire dai potenziali scalare (o elettrico) e vettore validi nei casi stazionari, e che tengono conto del fatto che gli effetti dovuti a variazioni delle sorgenti si propagano nel campo non istantaneamente.

Il comportamento del dipolo oscillante è governato dalla seguente relazione:

${\displaystyle \mathbf {p} =\mathbf {p} _{0}\sin(\omega t \phi )}$

dove ${\displaystyle \mathbf {p} _{0}}$, il momento di dipolo massimo del dipolo oscillante, è diretto come l'asse z. Il potenziale vettore ritardato generato dal dipolo è fornito dall'integrale sulle variabili primate, con tau il volume del conduttore di cui è formato il dipolo:

${\displaystyle \mathbf {A} (\mathbf {r} ,t)=\int {\frac {\mu _{0}}{4\pi }}{\frac {\mathbf {J} \left(t-{\frac {|\mathbf {r} -\mathbf {r} \,'|}{c}}\right)}{|\mathbf {r} -\mathbf {r} \,'|}}\operatorname {d} \tau '}$

Il campo di maggiore interesse è quello lontano dal dipolo, e pertanto si trascura ${\displaystyle \mathbf {r} \,'}$ rispetto a ${\displaystyle \mathbf {r} }$, che diventa una costante e viene estratto dall'integrale. Il risultato che si ottiene è:

${\displaystyle \mathbf {A} (\mathbf {r} ,t)={\frac {\mu _{0}}{4\pi }}{\frac {{\dot {\mathbf {p} }}\left(t-{\frac {r}{c}}\right)}{r}}={\frac {\mu _{0}}{4\pi }}{\frac {\omega \mathbf {p} _{0}}{r}}\cos \left(\omega (t-{\frac {r}{c}})\right)}$

Imponendo la validità del gauge di Lorenz si mostra il potenziale scalare ${\displaystyle V}$:

${\displaystyle {\frac {\partial V}{\partial t}}=-c^{2}\mathbf {\nabla } \cdot \mathbf {A} =-{\frac {1}{\varepsilon _{0}\mu _{0}}}{\frac {\partial A_{z}}{\partial z}}={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {\ddot {p}}{cr}} {\frac {\dot {p}}{r^{2}}}\right){\frac {z}{r}}}$

${\displaystyle V(\mathbf {r} ,t)={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {\dot {p}}{cr}} {\frac {p}{r^{2}}}\right){\frac {z}{r}}}$

I campi elettrico e magnetico generati dal dipolo si ottengono dal rotore di ${\displaystyle \mathbf {A} }$ e dal gradiente di ${\displaystyle V}$. In coordinate sferiche, essi prendono la forma:

${\displaystyle E_{r}={\frac {2\cos \theta }{4\pi \varepsilon _{0}r^{2}}}\left({\frac {\dot {p}}{c}} {\frac {p}{r}}\right)\qquad B_{r}=0}$

${\displaystyle E_{\theta }={\frac {\sin \theta }{4\pi \varepsilon _{0}r}}\left({\frac {\ddot {p}}{c^{2}}} {\frac {\dot {p}}{cr}} {\frac {p}{r^{2}}}\right)\qquad B_{\theta }=0\ }$

${\displaystyle E_{\phi }=0\qquad B_{\phi }={\frac {\mu _{0}}{4\pi }}{\frac {\sin \theta }{r}}\left({\frac {\ddot {p}}{c}} {\frac {\dot {p}}{r}}\right)}$

Da queste espressioni si vede come ${\displaystyle \mathbf {E} }$ e ${\displaystyle \mathbf {B} }$ siano punto per punto ortogonali. Le linee di forza di ${\displaystyle \mathbf {B} }$ sono circonferenze centrate intorno all'asse z, mentre ${\displaystyle \mathbf {E} }$ giace nel piano formato dal raggio vettore ${\displaystyle \mathbf {r} }$ e z.

Vettore di Poynting ed equazione di Larmor

Per calcolare l'energia associata ai campi si utilizza il vettore di Poynting:

${\displaystyle \mathbf {S} =\mathbf {E} \times {\frac {\mathbf {B} }{\mu _{0}}}}$

le cui componenti sono:

${\displaystyle S_{r}={\frac {\sin ^{2}\theta }{16\pi ^{2}\varepsilon _{0}c^{3}}}\left({\frac {\ddot {p}}{r}}\right)^{2}-{\frac {1}{16\pi ^{2}\varepsilon _{0}}}\left[2{\frac {{\ddot {p}}{\dot {p}}}{c^{2}r}} {\frac {{\dot {p}}p}{r^{3}}} {\frac {({\ddot {p}}p {\dot {p}}^{2})}{cr^{2}}}\right]{\frac {\sin ^{2}\theta }{r^{2}}}}$

${\displaystyle S_{\theta }={\frac {1}{16\pi ^{2}\varepsilon _{0}}}\left[{\frac {{\ddot {p}}{\dot {p}}}{c^{2}r}} {\frac {{\dot {p}}p}{r^{3}}} {\frac {({\ddot {p}}p {\dot {p}}^{2})}{cr^{2}}}\right]{\frac {2\sin \theta \cos \theta }{r^{2}}}}$

${\displaystyle S_{\phi }=0}$

Calcolando la media temporale della componente radiale su un periodo, i termini delle parentesi quadre si annullano e la media del vettore è:

${\displaystyle \langle \mathbf {S} \rangle ={\frac {\sin ^{2}\theta }{32\pi ^{2}\varepsilon _{0}c^{3}}}\left({\frac {\ddot {p}}{r}}\right)^{2}{\hat {r}}}$

I termini che si annullano nell'operazione di media non contribuiscono invece alla propagazione e sono detti termini di campo vicino. La potenza media irraggiata vale:

${\displaystyle \langle P\rangle ={\frac {\omega ^{4}p_{0}^{2}}{2}}{\frac {\mu _{0}}{6\pi c}}={\frac {\mu _{0}}{6\pi c}}{\bar {\ddot {p}}}^{2}}$

mentre la potenza totale emessa è data da:

${\displaystyle P={\frac {\omega ^{4}|\mathbf {p} |^{2}}{12\pi \varepsilon _{0}c^{3}}}}$

nota anche come equazione di Larmor.

Note

Bibliografia

• (EN) John D. Jackson, Classical Electrodynamics, 3ª ed., Wiley, 1999, ISBN 0-471-30932-X.

Voci correlate

• Antenna a dipolo
• Dipolo elettrico
• Antenna a dipolo
  • Dipolo equivalente
  • Dipolo hertziano
• Equazione di Larmor
• Gauge di Lorenz
• Potenziali ritardati
• Sviluppo in multipoli
• Vettore di Poynting